随着国家油气开采项目逐渐从东部转向西部,大尺度、大规模正演模拟就称为了地震数据处理中的必要环节,如何高效的进行正演模拟是地震数据处理问题的关键。有限差分方法由于其高效,简单的特性,成为了应为最为广泛的地震数值模拟技术之一。然而,当使用有限差分方法进行地震波传播模拟时,较大的空间或时间采样间隔可能导致频散误差和不稳定。在有限差分方法中,有限差分系数是决定频散误差和稳定性的关键因素。因此,如何获得适当的有限差分系数以保证最小的频散误差并确保数值模拟过程的稳定性是至关重要的
本文综述了基于三种不同计算理念的有限差分系数计算策略:窗函数策略、优化策略和泰勒展开策略。每种策略都有其独特的优点和局限性。
窗函数策略:通过截断伪谱方法的空间卷积序列来获取有限差分系数。尽管这种方法能够减少空间频散误差,但有限差分系数的带宽和频散误差难以通过输入参数控制。此外,窗函数策略主要关注空间频散误差,而不涉及时间频散误差。
优化策略:通过优化算法求解最优问题来获取有限差分系数。这种策略可以在给定误差限制和固定阶数的有限差分算子下最大化覆盖带宽。例如,雷米兹交换算法可以最大化有限差分系数带宽。然而,这种方法的计算成本较高,可以通过减少迭代次数或使用全局求解技术(如最小二乘方法)来降低计算成本。
泰勒展开策略:利用泰勒展开在零波数处展开频散关系,从而获得有限差分系数。这是获取有限差分系数的最简单方法,通常称为传统有限差分系数。通过泰勒展开,可以同时减小空间和时间频散误差。
通过对这三种策略进行详细的比较分析,我们发现每种策略在不同的应用场景下都有其优势。例如,对于易模拟不稳定的高速体而言,可以采用频散误差较小,但是稳定性较好的泰勒展开方法;对于易产生频散的低速体而言,则可以采用优化策略进行频散误差的压制。此外,我们还探讨了这些方法在未来研究中的潜在方向,包括提高有限差分系数的稳定性和减小低波数区域的频散误差。
为了验证这些策略的有效性,我们进行了多个数值实验和分析测试。结果表明,这些策略在地震波模拟中是非常有用的工具,尤其是在处理大规模或多尺度结构的问题时。特别是,拓宽覆盖带宽以改善模拟结果已经被数学证明是有效的。未来的研究热点将集中在如何减小低波数区域的频散误差以及如何提高有限差分稳定性。
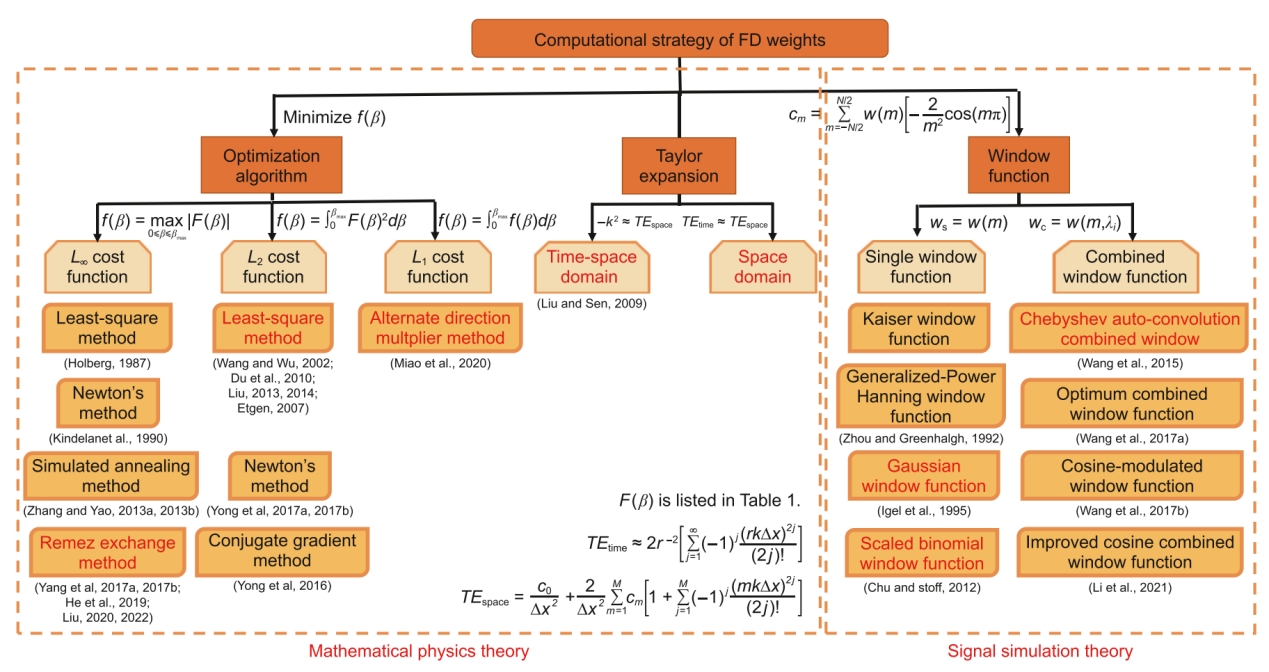
图1.有限差分系数的计算策略图
研究成果近期发表在石油科学领域国际重要期刊Petroleum Science。论文第一作者为米兰网页版黄建平教授,通讯作者为米兰网页版彭炜颋博士。
论文信息:Jian-Ping Huang, Wei-Ting Peng*, Ji-Dong Yang, Lu-Feng Lou, 2024, Overview of computation strategies on the dispersion analysis for explicit finite difference solution of acoustic wave equation. Petroleum Science, https://doi.org/10.1016/j.petsci.2024.02.003.





